FRAZIONI SUL FILO > FASE 4 > ATTIVITÀ 1 > ATTIVITÀ 2 > ATTIVITÀ 3

 

ATTIVITÀ 3

Con questo percorso gli studenti sviluppano una grande familiarità con i numeri razionali che consente loro di gestire, senza particolari difficoltà, le operazioni tra frazioni.

In particolare, a questo punto del percorso, gli studenti riescono già a sommare (nel senso di somma algebrica) le frazioni, anche senza spiegazioni specifiche o l'introduzione di "regole" da parte dell’insegnante, essendo già abituati a trovare frazioni equivalenti opportune. Per sommare frazioni con denominatori diversi procedono, quindi, scegliendo un multiplo comune ai denominatori e trovando le frazioni equivalenti che abbiano quel numero come denominatore, per poi sommare tra loro i numeratori. Si invita pertanto l’insegnante a proporre agli studenti alcune somme e chiedere a loro come si possano calcolare: nelle classi sperimentali varie strategie sono emerse spontaneamente dagli studenti a questo punto del percorso didattico.

Per quanto riguarda il prodotto, proponiamo di presentarlo agli studenti attraverso una serie di attività da fare in classe in cui si costruisce il significato di “frazione di frazione” facendo riferimento direttamente alla retta dei numeri. Alla luce del percorso fatto, che ha portato a costruire e ad acquisire familiarità nel trattare la frazione come numero, non suggeriamo l’uso dell’artefatto tovaglietta per lavorare sulla moltiplicazione attraverso le aree. Proponiamo, invece, di continuare il percorso lavorando con le frazioni sulla retta dei numeri.

Per esempio: calcolare un mezzo di un mezzo

 

 

Questo approccio, basato sulla rappresentazione visiva, permette agli studenti di costruirsi un’immagine mentale coerente con il significato della traduzione dall’italiano “un mezzo di” alla moltiplicazione “un mezzo per”.

Osserviamo che in questo passaggio alla moltiplicazione è molto importante non perdere di vista quale sia l’intero di riferimento, ed è compito dell’insegnante, durante la discussione in classe, riprendere e sottolineare questo aspetto.

Inoltre, possiamo mostrare la commutatività della moltiplicazione, sempre sfruttando il posizionamento delle frazioni sulla retta dei numeri.

Per esempio: calcolare due terzi di un mezzo

 

 

Dopo aver visto una serie di esempi, che l’insegnante può via via riassumere alla lavagna in scrittura matematica, gli studenti si accorgono delle regolarità e formulano spontaneamente la regola generale della moltiplicazione tra frazioni.

Per quanto riguarda la divisione si può procedere esattamente allo stesso modo, sempre lavorando sulla retta dei numeri.

Per esempio: calcolare un mezzo diviso tre

 

 

Per esempio: calcolare tre diviso un quarto

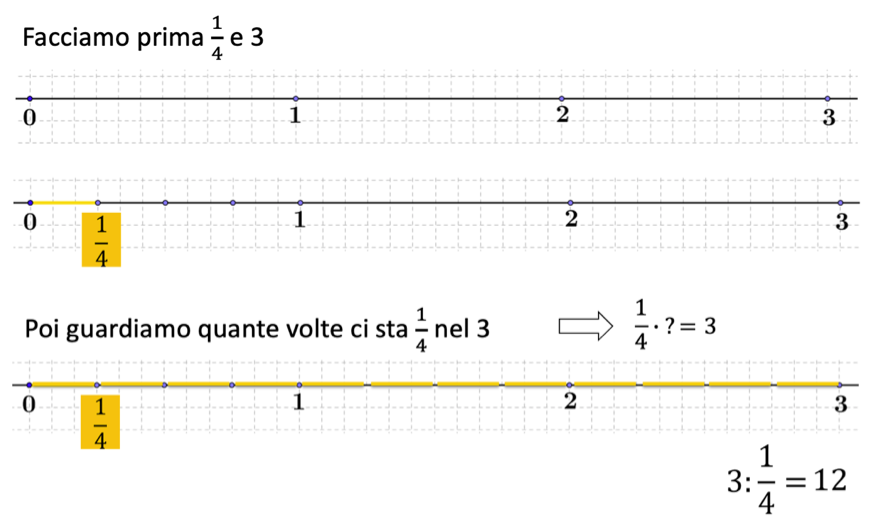
Osserviamo che l’idea alla base di questo ragionamento è quella di trovare un nuovo numero che moltiplicato per il divisore dia il dividendo. Quindi 3 : diventa trovare un numero che moltiplicato per dia 3. Analogamente possiamo procedere per calcolare un mezzo diviso un ottavo. Per guidare la discussione e, soprattutto, per aiutare gli studenti a formalizzare questo ragionamento, che consiste nel trasformare la divisione in una moltiplicazione, suggeriamo all’insegnante di scrivere alla lavagna l’operazione "bucata" corrispondente (si veda l’immagine).

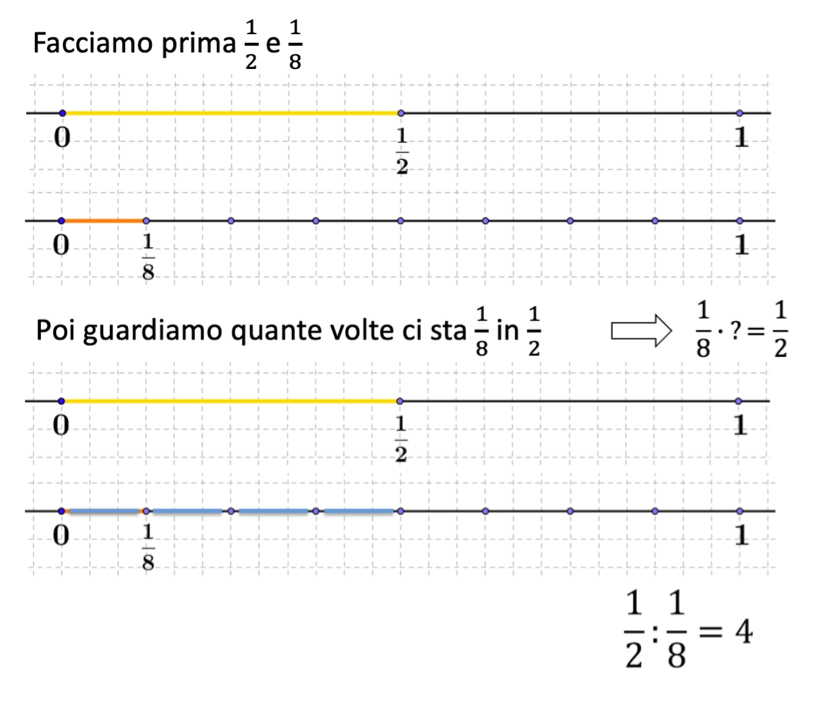
Nuovamente, l’insegnate produrrà diversi esempi di divisioni tra frazione e numero naturale ma anche tra due frazioni, e li riassumerà alla lavagna uno sotto l’altro. Gli studenti saranno invitati a trovare una regola pratica (e saranno curiosi di farlo in modo autonomo) per gestire l’operazione senza il supporto della retta. Il passaggio all’astrazione della regola risulta, invece, meno immediato rispetto al caso della moltiplicazione. Inizialmente gli studenti parlano spesso di "moltiplicare numeratori e denominatori in maniera incrociata". Dunque sarà importante che l’insegnante espliciti la scelta dei matematici di trasformare la divisione per un divisore nella "moltiplicazione per il reciproco" di tale divisore.

Nelle classi sperimentali, sono state riscontrate alcune difficoltà comuni nel calcolo con le frazioni, messe in luce anche nella letteratura: in qualche caso le regole per il prodotto e per la somma tra frazioni sono state confuse, in particolare laddove le frazioni non erano ridotte ai minimi termini. Tuttavia, avendo gli studenti costruito il significato che sta alla base della regola, nel correggersi vicendevolmente, si appoggiavano a quello andando a recuperarlo attraverso l’uso della retta. Questo è un aspetto rilevante per l’apprendimento, anche a lungo termine.

 

Vai alle Conclusioni della Fase 4 ➜

 

2018_3_1011_IP.01 “LE NUOVE FRONTIERE DEL DIRITTO ALL’ISTRUZIONE. Rimuovere le difficoltà d’apprendimento, favorire una scuola inclusiva e preparare i cittadini responsabili e attivi del futuro - Fase 2". Questa iniziativa è realizzata nell'ambito del Programma operativo FSE 2014 – 2020 della Provincia autonoma di Trento grazie al sostegno finanziario del Fondo sociale europeo, dello Stato italiano e della Provincia autonoma di Trento. La Commissione europea e la Provincia autonoma di Trento declinano ogni responsabilità sull’uso che potrà essere fatto delle informazioni contenute nei presenti materiali.