FRAZIONI SUL FILO > FASE 1 > ATTIVITÀ 1

 

ATTIVITÀ 1

L’insegnante, dopo aver distribuito i fogli A4 bianchi e spiegato alla classe la consegna, lascia alcuni minuti per lavorare individualmente. Mentre gli studenti lavorano, l’insegnante gira tra i banchi e osserva le varie strategie utilizzate per la suddivisione (pieghe, righello, forbici). L’obiettivo è che gli studenti della classe dividano il foglio in vari modi così da ottenere unità frazionarie di forma diversa. Nel caso ciò non avvenisse, si può spronarli ad essere originali!

Per velocizzare l’attività, è possibile suddividere gli studenti in tre gruppi, assegnando ad esempio alla prima fila la suddivisione in mezzi, alla seconda fila la suddivisione in quarti e all’ultima fila quella in terzi (solitamente la più soggetta ad errori).

Si invita l’insegnante a fare attenzione ad alcuni errori ricorrenti. Ad esempio, se qualcuno utilizza il righello potrebbe essere invogliato a ritagliare una strisciolina, mettendola da parte, per arrotondare le misure del foglio A4 che non sono intere (21cmx29,7cm). Questo è un aspetto interessante da riprendere nella discussione. Il foglio A4, infatti, costituisce l’unità di misura fissata – la tovaglietta – e con questa attività si vuol costruire l’unità frazionaria attraverso la suddivisione in parti uguali dell’intero. Tagliando un pezzo di foglio, si varia l’unità di misura.

Alla richiesta di suddividere il foglio in parti uguali, ogni studente procederà a suo modo ottenendo così unità frazionarie di forma diversa. La discussione in classe si concentra sull’equivalenza delle varie unità frazionarie create, a prescindere dalla loro forma. Tale equivalenza, se necessario, è verificabile in modo cinestetico-tattile attraverso forbici, pieghe, isometrie (rotazioni, traslazioni, sovrapposizioni...). Occorre a questo punto fare una riflessione sull’uso e sul significato di alcune parole in matematica.

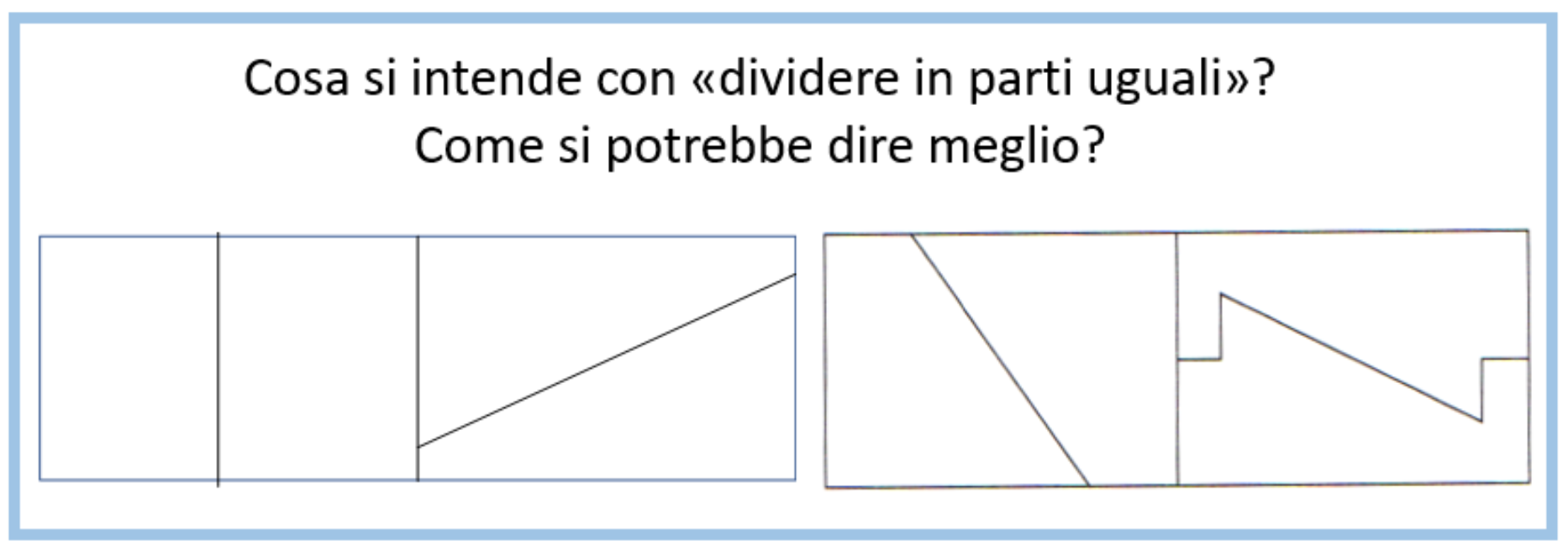
L’obiettivo principale della discussione è fare chiarezza sull'uso della parola “uguale” in questo contesto. Spesso questa parola è usata con il significato di “congruente”. È molto importante quindi discutere con gli studenti la differenza tra congruente (uguale come forma e area), simile (uguale come forma, tipo zoom) ed equivalente (uguale come area).

 

Cosa aspettarsi

L’insegnante raccoglie alcuni lavori opportunamente scelti e chiede, ad esempio, se due diverse realizzazioni di “mezzi” possono o meno considerarsi uguali. Si può scegliere di mettere a confronto un “mezzo” a forma rettangolare, con uno a forma triangolare o trapezoidale. 

Solitamente basta questo per innescare una bella discussione tra gli studenti. Nella maggior parte dei casi la classe si divide in tre gruppi: gli studenti convinti del sì, quelli convinti del no e quelli che rispondono “dipende”. Sono quest’ultimi a iniziare ad insinuare alcuni dubbi perché argomentano che dipende da cosa si prende in considerazione, se l’area oppure la forma.

A questo punto l’insegnante può chiedere quale di queste due interpretazioni sia importante per il concetto di frazione e rilanciare nuovamente la palla alla classe. A seconda del lavoro svolto dagli studenti alla scuola primaria, qualcuno potrebbe essere convinto che dividere in parti “uguali” una superficie sia necessariamente legato ad ottenere parti tra loro congruenti, altri potrebbero accettare l’idea che le parti siano “solo” equivalenti, cioè equiestese. Il confronto tra questi due gruppi è indispensabile per fare chiarezza sull'uso della parola “uguale” e superare uno dei principali ostacoli didattici legato al significato di frazione come parte-tutto.

Nella fase iniziale dell’attività è importante che l’insegnante colga se ci sono stati errori nella suddivisione dei fogli. Solitamente, alla scuola secondaria, gli errori emergono solo nella realizzazione dei “terzi” e i più comuni sono:

- le parti non sono equivalenti, spesso per poca precisione;

- è stata modificata l’unità di partenza (foglio A4).

Come già riferito, il secondo errore merita una discussione collettiva perché è importante capire che il foglio viene scelto come unità di misura e che non è possibile modificarla se si vuole confrontare tra loro le varie unità frazionarie.

 

Vai all'Attività 2 ➜

 

2018_3_1011_IP.01 “LE NUOVE FRONTIERE DEL DIRITTO ALL’ISTRUZIONE. Rimuovere le difficoltà d’apprendimento, favorire una scuola inclusiva e preparare i cittadini responsabili e attivi del futuro - Fase 2". Questa iniziativa è realizzata nell'ambito del Programma operativo FSE 2014 – 2020 della Provincia autonoma di Trento grazie al sostegno finanziario del Fondo sociale europeo, dello Stato italiano e della Provincia autonoma di Trento. La Commissione europea e la Provincia autonoma di Trento declinano ogni responsabilità sull’uso che potrà essere fatto delle informazioni contenute nei presenti materiali.